
Available Works


ding musa_unit of construction-flexible_2019

ding musa_unidade de contrução_2019
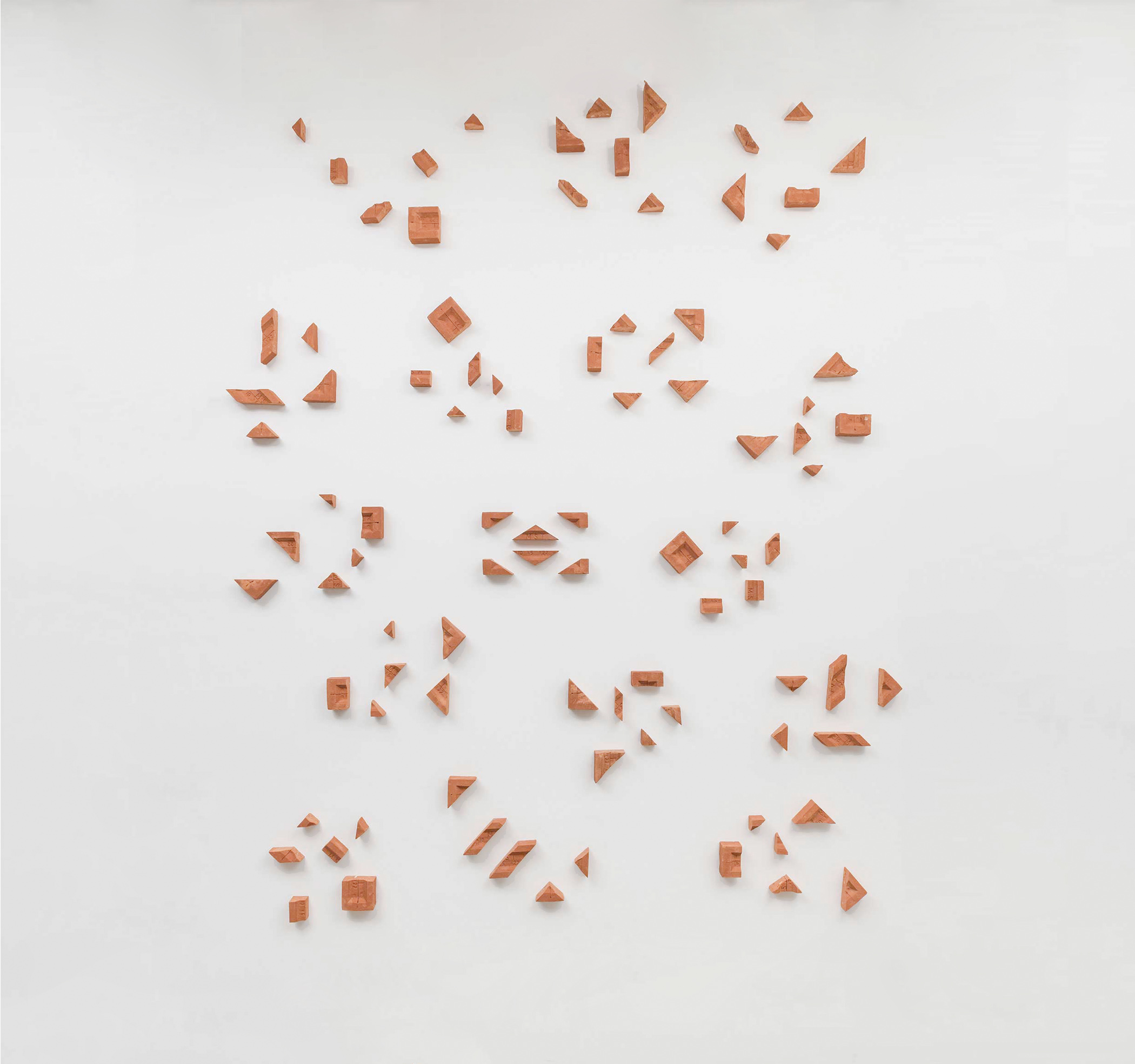
ding musa_tangram painel_2019

ding musa_resonances_2015

ding musa_arrangment (contract) social_2022

ding musa_untitled_2022

ding musa_queimada 1 horizonte_2022
Biography
born in são paulo_ brazil_ 1979_ lives and works in são paulo
Ding Musa studied music and geography at the University of São Paulo and graduated in photography at Senac. Although centered in photography, his work extends to other mediums such as video, drawing and installation. As of 2002, he began showing at both national and international exhibitions. Participated in several artist residencies, such as tactileBOSCH (Cardiff, Wales) in 2004, Carpe Diem Arte e Pesquisa (Lisbon, Portugal) in 2012 and C.A.J. Artist In Residence Program (Tokyo, Japan) in 2015. He taught history of photography courses at Senac and Sesc Santana, in 2009 and 2010, respectively. He has also worked as director of photography for movies, short films, series and documentaries, including “Campo da Paz” (Field of Peace) – a feature film set in Palestine.
Musa’s work is in various museums in Brazil and several collections abroad, among them the Museu de Arte Moderna in Salvador, in São Paulo, in Rio de Janeiro and in Fortaleza (Centro Dragão do Mar), the Museu de Arte Contemporânea de Goiás, the Museu de Arte Contemporânea do Paraná, the Museu do Estado do Pará, the Salão de Arte de Ribeirão Preto and the Centro Cultural São Paulo. Recently, two museums, the Museu de Arte Contemporânea da Universidade de São Paulo and the Museu de Arte do Rio Grande do Sul, acquired series of artworks by the artist. Galeria Raquel Arnaud represents the artist since 2014, the same year when the solo exhibition Equações was presented at the gallery.
Exhibitions

ding musa_every gaze is political
06 fev - 22 mar_2025

ding musa- equations
nov 26 - dec 20_2014

raid _8 (redundant array of independent disks)
aug 18 - oct 22_2016
Texts
Singly or in pairs, with parallelisms or mirror images, the recent work of Ding Musa calls to mind equations – chemical formulae, algebraic proportions, geometric equivalences, and equilibria of forces. They are fundamental notations in all schooling because they enable us to express, quantify and calculate relationships between more or less abstract volumes.
The systems of perception elaborated by Ding Musa (usually photographs, though they may also be objects, installations or videos) share with equations the comparison between two or more sets as equivalents, although they may be asymmetrical. That is to say, if there is an equal sign, an arrow or other sign in the middle of a formula, that is because it is possible to join two sets through some relationship of equality, transformation, reaction, etc. If a=a’, it is because a and a’ are comparable, but also sufficiently different to justify the existence of the equation.
So if we see an image composed of two practically identical photographic records, equal frames of a tiled wall in which a mirror reflects another section of white tiles, we quickly understand that a (the left portion of the photo) is equal to a’ (the right portion). But would it actually be necessary to prove this equality that is so obvious with such a photographic equation? Would it be necessary to print these images as one? Perhaps it would, above all if we notice that they are not in fact identical. First, because of the difference between the photographic acts: one places tiles on the wall in focus, the other shifts the focal distance between the lenses to stop at the other tiles, those reflected by the mirror. The difference, since they are such similar surfaces, is a subtle one, it gets mixed up with the delicate change of focus that our eyes undergo at all times to maintain awareness of the depth they are discerning. The discreet asymmetry of these images makes palpable a real spatial volume described in a planar and 2-dimensional photographic surface.
Then, there is a difference in the same surface between the two parts of the image. It’s what appears with scratches, dark spots, miniscule flaws that could be stains on the whiteness of the tiles, dust floating in front of the lens, or even imprecisions of the paper and printing. It doesn’t matter, because what they reveal is the fallibility of the materials when prompted to correspond with abstract ideas. There are distinct fissures in each half of the work, which demonstrate that, even when organized as an equation, the materiality of the real resists abstraction.
Many of the works at Ding Musa’s exhibit, chiefly when there are two or more similar parts, invite the spectator to scrutinize possible differences between them, perceiving relationships of apparent equivalence and the infinite inequality that reality brings. It is a practice that would also foster suspicion of the flawed “exactness” that education applies to fields of knowledge with greater affinity for formulae and equations.
But the difference between two things is not always the active principle in the work of Ding Musa. Sometimes we look at a unity, such as the work that opens the exhibit: a circle made of threaded mud, also called “infinite screw,” through whose length a screw can be inserted, a “nut.” Here there are no such obvious comparisons. They are brimming with metaphors of unity. The circle and the dot. The representation of the hydrogen atom. The snake (the bar) that becomes infinite when it swallows its own tail. If it were an equation, it could be a function in which b -> b, that is, in which something tends towards itself. Or else, in which b tends towards the infinite (positive or negative). Clearly there is some kind of hustle or trick here, because otherwise, how would the nut have entered onto the bolt without any loose ends? The fact is that no equation is truly finite and closed. Its fissure appears at the limit of the probable. And the improbability of perfection becomes stronger later on, at the end of the room, when this work is encountered for a second time, identical but different. The artist Jeff Wall said that if photography had to be compared to a literary form, it would be with poetry in prose. In the case of Ding Musa’s work, we might think in palindromes and poems of symmetrical structure, or, looking at a set of several works, think of stories of fantastic literature with a circular narrative, in which we end more or less where we start from, only transformed.
As far as its compositional organization is concerned, the work is sometimes reminiscent of pictorial forms, constructive schemes with their planes of color, rhythms and diagonals. At these times, it’s not an accident, nor is it something that “justifies” the works. It would be plausible to think that this happens because Ding has in common with the tradition of constructive concrete art of the 1950’s and 60’s an interest in logical thinking organized in simple equations, which for this very reason looks for friction with the geometric design. The difference is that, while in the former context the logic must remain pure, barely shaded by intuition, in the present context it is shown to demonstrate its limitations and fissures, subtle though they may be.
It behooves each observer of these works to undertake a certain task of reasoning and logical projection, oriented by the compositional conciseness of the works assembled. If, at the end, everything seems highly mathematical, it is possible to start all over again and simply play “find seven mistakes,” as in the puzzle section of newspapers once upon a time. At all events, it’s best not to forget that even the slightest differences, if we observe them very closely, at the boundary, tend towards the infinite.





































